论文信息
论文:Adaptive Graph Convolutional Recurrent Network for Traffic Forecasting
会议:NIPS 2020
作者:

Introduction
摘要
在相关的时间序列数据中对复杂的空间和时间相关性进行建模对于理解交通动态并预测不断发展的交通系统的未来状态是必不可少的。 最近的工作专注于设计复杂的图神经网络,以借助预定义的图捕获共享模式。在本文中,作者认为,学习节点特定的模式对流量预测至关重要,同时可避免使用预定义的图
为此,本文提出了两个具有新功能的自适应模块来增强图卷积网络(GCN): 1)一个节点自适应参数学习(NAPL)模块来捕获节点特定模式;2)数据自适应图生成(DAGG)模块,自动推导出不同交通序列之间的依赖关系。
我们进一步提出了一种自适应图卷积递推网络(AGCRN),以自动捕获流量序列中细粒度的空间和时间相关性。我们在两个真实世界流量数据集上的实验表明,在没有预先定义空间连接图的情况下,AGCRN的表现明显优于最先进的技术
Motivation
特定模式
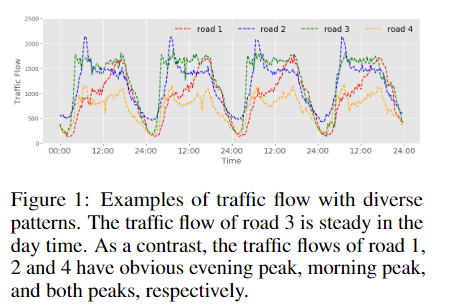
事实上,交通序列呈现出多种多样的模式(如图1所示),由于不同数据源的属性不同,可能出现相似、不相似甚至矛盾的情况。下图具有不同模式的交通流示例。 白天,道路3的交通流量稳定。 相比之下,道路1,2和4的交通流量分别具有明显的傍晚高峰,早晨高峰和两个高峰。
预先定义的图
此外,现有的基于GCN的方法需要通过相似性或距离度量[14]预先定义互连图以捕获空间相关性。 这进一步需要大量的领域知识,并且对图形质量敏感。 以这种方式生成的图形通常是直观的,不完整的,并且并非直接针对预测任务。 它们可能包含偏见,并且在没有适当知识的情况下无法适应领域
Contribution
没有设计更复杂的网络体系结构,而是通过设计当前方法(GCN)的基本模块来分别解决上述问题,本文提出了两种简洁而有效的机制。 具体来说,本文使用两个自适应模块来增强GCN,以进行流量预测任务:
-
节点自适应参数学习(NAPL)模块,用于学习每个流量系列的特定于节点的模式,NAPL对传统GCN中的参数进行分解,并根据节点嵌入从所有节点共享的权重池和偏差池中生成特定于节点的参数
-
一个数据自适应图生成(DAGG)模块,用于从数据中推断节点嵌入(属性)并在训练期间生成图
NAPL和DAGG是独立的,可以分别或联合用于现有的基于GCN的流量预测模型。 可以轻松地以端到端的方式学习模块中的所有参数。 此外,我们将NAPL和DAGG与递归网络相结合,并提出了统一的流量预测模型-AdaptiveGraph卷积递归网络(AGCRN)
Methodology
Problem Definition
N个相关单变量交通流量时间序列,长为t:
图
表示结点集合,$$\mathcal{E}$$表示边集合,$$\boldsymbol{A}$$是表示交通节点连接关系的邻接矩阵
目标:
使用过去$$T$$个时刻的交通流量数据,预测未来$$\tau$$个时刻的流量数据
problem
Node Adaptive Parameter Learning
图卷积
注
表示邻接矩阵, 表示度矩阵, 表示图卷积层的输入和输出
表示图卷积的参数(weights and bias)
作用
使用共享的参数完成节点特征的变换:
问题
**共享参数可能有助于在许多问题中学习所有节点中最突出的模式,并能显著减少参数数,但对于交通预测问题,我们发现共享参数不是最优的。**除了封闭相关交通序列之间存在密切的空间相关性外,由于时间序列数据的动态适宜性以及节点的各种影响交通的因素,**不同交通序列之间也存在着不同的模式。**来自两个相邻节点的流量流也可能由于其特定属性(如PoI、天气)而在某一特定时段呈现不同的模式。另一方面,来自两个不相交节点的交通量甚至可能显示相反的模式。 结果,仅捕获所有节点之间的共享模式不足以进行准确的流量预测,并且必须为每个节点保持唯一的参数空间以学习特定于节点的模式。
Node Adaptive Parameter Learning module
为什么要用这个模块?
为每一个节点分配参数 => ,会导致参数量巨大难以优化,同时造成 over-fitting
方法
- 不直接学习,设计一个可以学习的节点嵌入,以及权重池,来生成。
- 理解为利用节点的嵌入从权重池中提取参数,这样每个节点都能学到独立的模式
Data Adaptive Graph Generation
预定义的图存在的问题
- 预先定义的图不能包含关于空间依赖的完整信息
- 不能保证预先定义的图与预测任务的直接关系
方法
随机初始化可学习的节点嵌入矩阵,通过矩阵运算来得出节点之间的依赖关系
使用DAGG的卷积公式如下所示:
Adaptive Graph Convolutional Recurrent Network
集成NAPL-GCN、DAGG和门控循环单元(GRU),以捕获流量级中特定节点的空间和时间相关性

Experiments
Datasets
-
PeMSD4
307个检测器
-
PeMSD8
170个检测器
Overall


- GCN对交通流量预测任务的重要性
- 本文提出的模型实现了5%的提升
消融实验
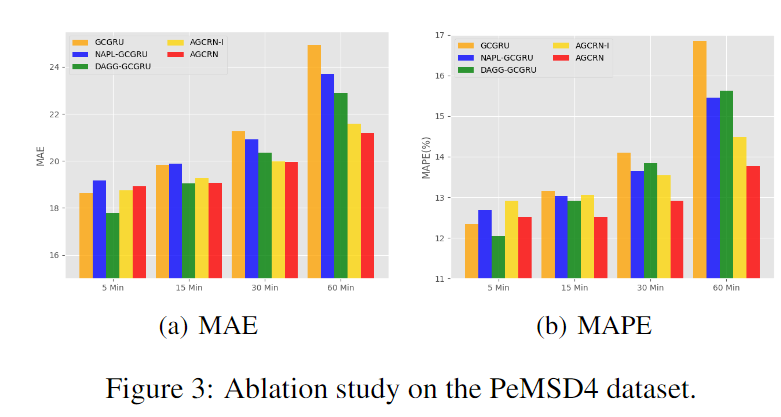
- GCGRU:GCN+GRU的传统模型
- NAPL-GCGRU:使用本文提出的NAPL替换了传统GCN的模型
- DAGG-GCGRU:使用本文提出的DAGG替换了传统GCN中的预定义图
- AGCRN-I 所有模块的节点嵌入不共享
- AGCRN 节点嵌入在所有模块中共享
- NAPL-GCGRU胜过GCGRU,AGCRN-1胜过DAGG-GCGRU,这说明捕获特定于节点的模式的必要性。NAPL主要增强长期预测,对短期预测的影响较小。论文推测,其原因是长期预测缺乏来自历史观测的足够有用的信息,因此从NAPL模块学习到的特定节点嵌入中获益,从而推断出未来的模式
- DAGG-GCGRU提升了GCGRU, AGCRN-I打败了NAPL-GCGRU。两者都显示了DAGG在推断空间相关性方面的优势。证明并不一定需要预定义的图
- AGCRN的性能最好,说明我们可以共享所有模块的节点嵌入,并从数据中学习到每个节点统一的节点嵌入。
Model Analysis
Graph Generation

- NAGG-r 去除了原本模型的中的自环连接
- NAGG-1 本文提出的方法
- NAGG-2 使用模仿2阶切比雪夫多项式
- 从DAGG中删除单位矩阵会严重损害预测性能,这表明在预测中手动突出显示自我信息的重要性
- DAGG-2和 DAGG-1的性能类似,表明生成的图拉普拉斯矩阵具有与切比雪夫多项式展开式中的预定义图相似的属性
Embedding Dimension

Computation Cost

(dim = 10性能最好)